이진탐색

04 May 2021

Reading time ~7 minutes

순차탐색

리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 확인

이진 탐색

이미 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색
- 이진 참색은 시작점, 끝점, 중간점을 이용하여 탐색 범위 설정
기본 소스 코드

수 찾기(백준 1920)

이분 탐색 진행 시 전체 범위를 나타내는 변수 설정
- 시작 : st, 끝 : en
범위를 절반으로 줄이기 위해 mid = (st+en)/2 지점을 생각
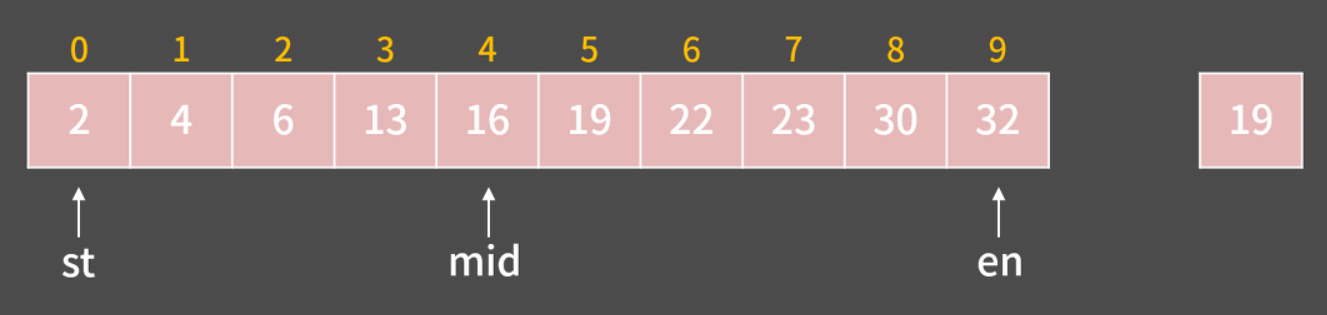
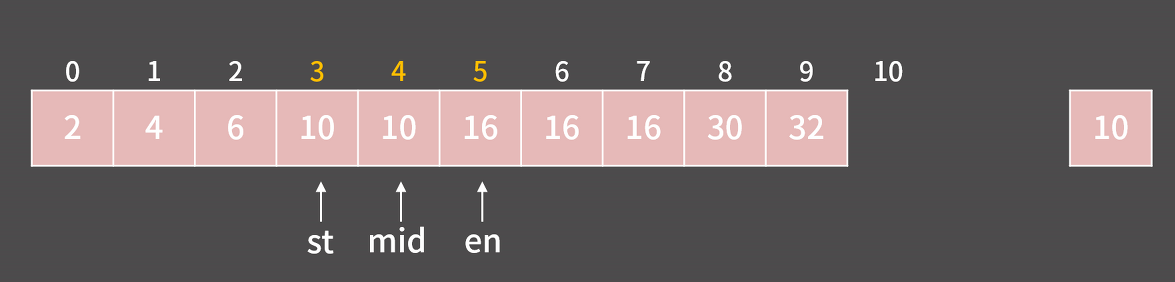
- st = 0, en = 9인 상황에서 mid = 4입니다. 우리는 A[mid]와 19의 값을 비교해 범위를, 즉 st 혹은 en의 값을 적절하게 바꿀 예정
A[mid] = 16인데 찾고 싶은 값은 19
- A[mid] < 19(target) 이기 때문에 st = mid+1로 변경 후 범위를 절반으로 줄일 수 있음

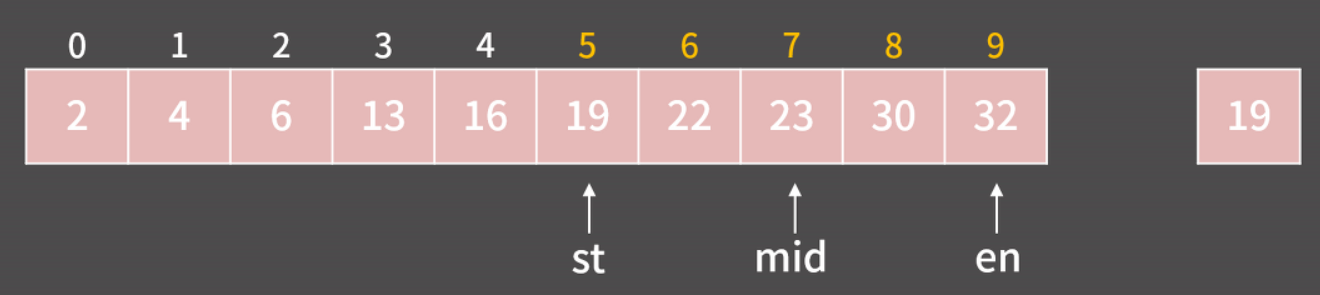
이제, A[mid] = 23이므로, A[mid] > 19이기 때문에, en = mid - 1로 변경
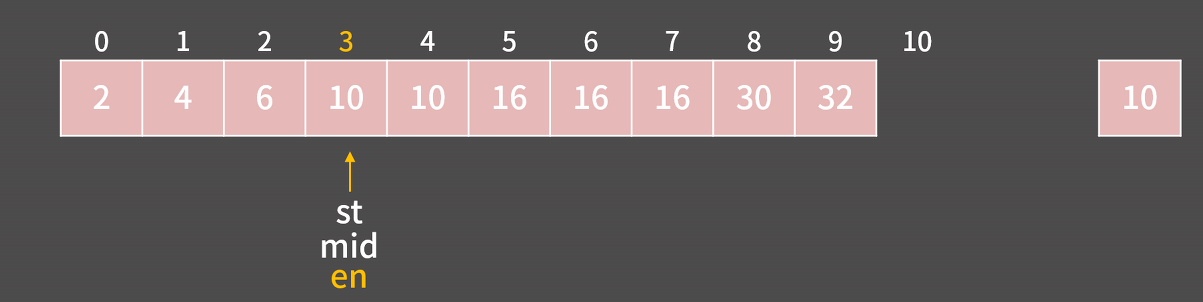
st = 5, en = 6이므로 A[mid] = 19(target)이므로 찾았다!
만약 target을 찾을 수 없다면?
- st, en, mid가 한 곳에 다 모이게 된다.
  - 이 때, st와 en이 역전이 되게 된다!
  - st와 en 사이의 값 또한 사라지게 됨
  - 따라서 배열 안에 target이 없음을 알 수 있음

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int a[100005];
int n;

int binarySearch(int target){
    int st = 0;
    int en = n - 1;
    while(st <= en){ //역전이 되면 target을 찾을 수 없기에 아래 return 0
        int mid = (st + en) / 2;
        if(a[mid] < target){
            st = mid + 1;
        }else if(a[mid] > target){
            en = mid - 1;
        }else{
            return 1;
        }
    }
    return 0;
}

int main(){
    cin >> n;
    for(int i=0; i<n; i++){
        cin >> a[i];
    }
    sort(a, a+n);
    int m;
    cin >> m;
    while(m--){
        int t;
        cin >> t;
        cout << binarySearch(t) << '\n';
    }

}

upper_boud와 lower_bound

용도 : 찾으려는 key 값보다 같거나 큰 숫자가 배열 몇 번째에서 처음 등장하는지 찾기 위함
- 핵심 원리 : 배열의 특정 index에 원소를 삽입
- 삽입할 원소가 주어질 때 오름차순 순서가 유지되는 가장 왼쪽 위치(lower_bound) 와 가장 오른쪽 위치(upper_bound)를 이분탐색으로 찾아낸다.
사용 조건 : 탐색을 진행할 배열 혹은 벡터는 오름차순 정렬되어 있어야 함

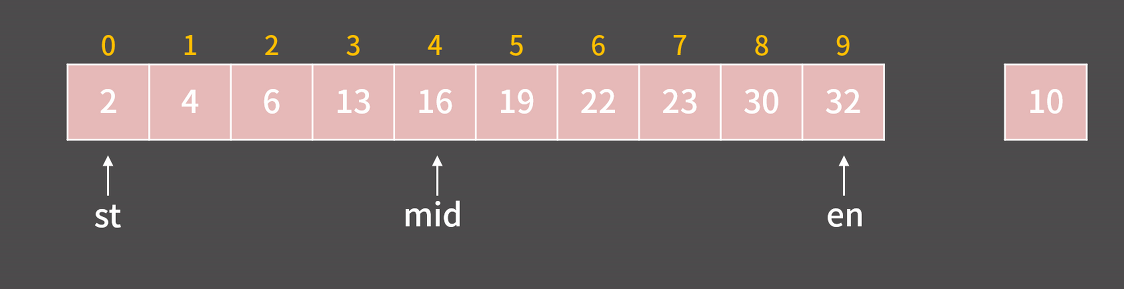
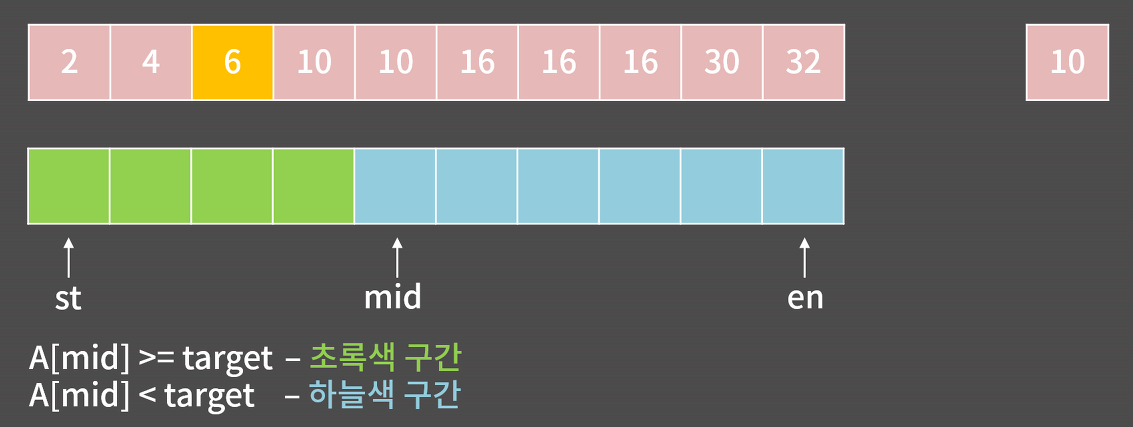
목표 : 목표 : 10이 들어갈 수 있는 가장 왼쪽 위치를 구하기

- A[mid] > 10 이기 때문에, 10이 들어갈 수 있는 가장 왼쪽 위치는
  - 배열안에 10이 있다면 10이 최초로 등장하는 위치
  - 10이 없다면 10보다 큰 수가 최초로 등장하는 위치
  - 10이 들어갈 수 있는 가장 왼쪽 위치는 A[mid] 이하 임을 알 수 있다.
  - 즉, mid가 10이 들어갈 수 있는 가장 왼쪽 위치일 수 있다는 것을 생각할 수 있어야 함
    - A[3] = 6, A[4] = 6이라하면, 10이 들어갈 수 있는 가장 왼쪽위치가 mid, 즉 5번째가 됨
  - 따라서, A[mid] > 10이면, en = mid로 변경함
- 위에서 다시, mid = (st + en) / 2 => A[mid] = 6이 됨, 이제 st와 en을 어떻게 해야할까?
  - A[mid] < 10 이기 때문에, 10이 들어갈 수 있는 가장 왼쪽 위치는
    - mid가 될 수 없고, mid보다 더 큰 인덱스들 중 하나일 것임
    - 따라서, st = mid + 1로 변경
- 다시, mid = (st + en) / 2 => A[mid] = 10이 됨, 이제 st와 en을 어떻게 해야할까?
  - A[mid] > 10 일 경우와 똑같이, mid가 10이 들어갈 수 있는 가장 왼쪽 위치일 수도 있고, mid이하 일수도 있음
  - 따라서, en = mid로 변경
- 다시, mid = (st + en) / 2 => A[mid] = 10이 되고 en = mid로 변경
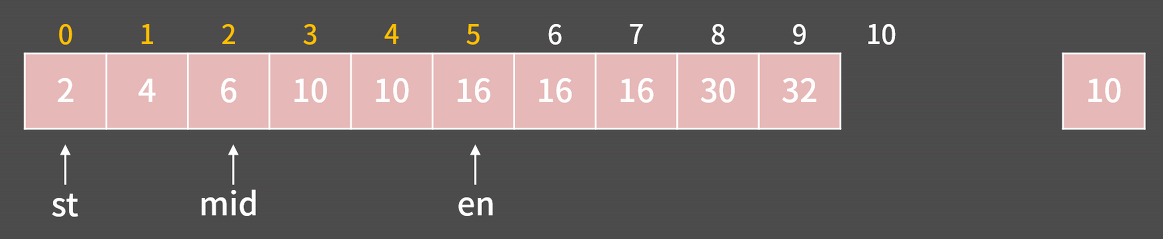
  - 이렇게, st = en이 되어서 가능한 후보가 1개가 되는 순간, 우리는 답을 찾은 것임!
    - 10이 들어갈 수 있는 가장 왼쪽 위치가 3번째임을 알 수 있음
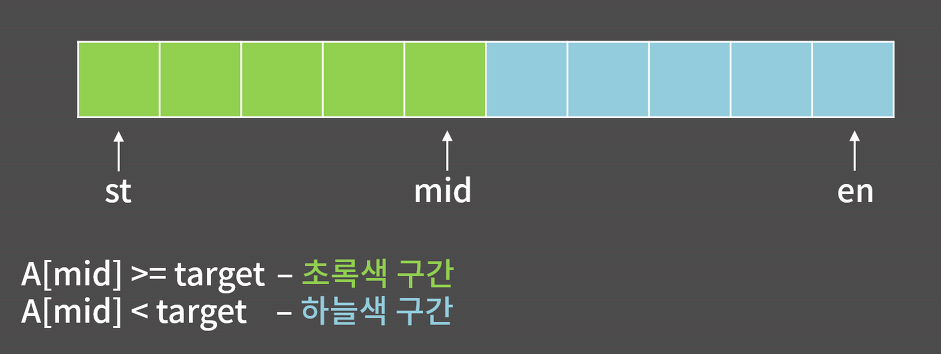
- 정리하면, A[mid] >= target 일때는 초록색 구간으로, en = mid 가 됨
- A[mid] < target 일 때는 하늘색 구간으로, st = mid + 1이 됨
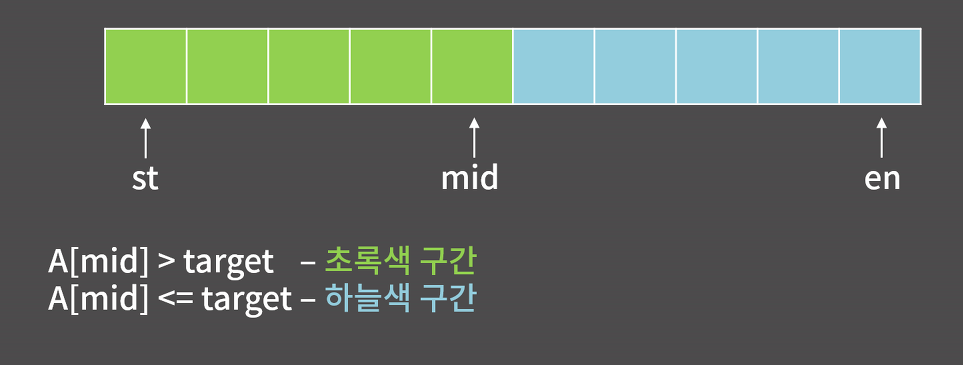
- 반대로, 10이 들어갈 수 있는 가장 오른쪽 위치를 구하는 과정은 A[mid] = target 일때만 달라짐!
  - A[mid] = target 일 때는 하늘색 구간인데, 왜냐하면 가장 오른쪽 위치는 target보다 큰 수가 최초로 나온 최초의 위치이기 떄문

lower_bound

en = len - 1이 아닌 en = len으로 두는게 중요(왜냐하면, 위 예제에서 삽입할 수 있는 위치는 0~9 까지가 아닌 0~10까지이기 때문)
STL

int lower_idx(int target, int len){
    int st = 0;
    int en = len;
    while(st < en){
        int mid = (st + en) / 2;
        if(a[mid] >= target){
            en = mid;
        }else{
            st = mid + 1;
        }
    }
    return st;
}

사용법 (배열)
- 첫번째와 두번째 인자는 범위 ```c++ #include #include using namespace std;

int main() {

int arr[6] = { 1,2,3,4,5,6 };
cout << "lower_bound(6) : " << lower_bound(arr, arr + 6, 6) - arr;

// 결과 -> lower_bound(6) : 5

return 0; } ```

사용법 (벡터)
- 벡터의 경우, 아래와 같이 v.begin()을 빼주면 됨

#include <iostream>
#include <algorithm>
using namespace std;

int main() {

	vector<int> arr = { 1,2,3,4,5,6,6,6 };
	cout << "lower_bound(6) : " << lower_bound(arr.begin(), arr.end(), 6) - arr.begin();

    // 결과 -> lower_bound(6) : 5
    
	return 0;
}

upper_bound

int upper_idx(int target, int len){
    int st = 0;
    int en = len;
    while(st < en){
        int mid = (st + en) / 2;
        if(a[mid] > target){ //lower_idx와의 차이점!! (위의 하늘색, 녹색 구간 참고)
            en = mid;
        }else{
            st = mid + 1;
        }
    }
    return st;
}

#include <iostream>
#include <algorithm>
using namespace std;

int main() {

	vector<int> arr = { 1,2,3,4,5,6 };
	cout << "upper_bound(3) : " << upper_bound(arr.begin(), arr.end(), 3) - arr.begin();

    // 결과 -> upper_bound(3) : 3
	return 0;
}

upper, lower Bound 활용 (해당 수를 몇개를 가지고 있는지?)

숫자 카드2 (백준 10816)
오름차순 정렬된 자료에서 특정 범위에 속하는 숫자들이 몇 개 있는지 탐색하고자 할 때

int main() {

	vector<int> arr = { 1,3,5,5,7,8,8,10,10,11,13 };
	cout << "5 이상 11 이하의 갯수 : " << upper_bound(arr.begin(), arr.end(), 11) - lower_bound(arr.begin(), arr.end(), 5);

	return 0;
}

int main() {

	vector<int> arr = { 1,3,5,5,5,8,8,10,10,11,13 };
	cout << "5의 갯수 : " << upper_bound(arr.begin(), arr.end(), 5) - lower_bound(arr.begin(), arr.end(), 5);

	return 0;
}

이분탐색 시 주의 사항

이분 탐색을 하고자 한다면 주어진 배열은 정렬되어 있어야 함!
무한 루프에 빠지지 않게 mid 값을 정해야 함
- 주어진 정렬된 배열에서 특정 원소를 찾거나, 삽입할 위치를 찾을 때는 STL을 쓰는게 편하지만,
- Parametric Search처럼 STL이 도움이 안되고 직접 이분탐색을 수행해야 하는 경우가 있음!
- 주어진 정렬된 배열에서 target보다 값이 작은 원소중에서 가장 오른쪽에 있는 원소를 찾는 상황을 생각해보자.
  - 이 예시에서는, 6이 된다. 생각해보면, lower_bound 함수의 반환값에서 한 칸 왼쪽으로 가면 되긴 한다.
  - 그런데, 직접 구현한다하면 st, mid, en 잡고 비교해 나갈텐데 위의 그림과 같이 초록과 하늘로 뉘어진다.
    - 지금까지 봐왔던 양상과 다르다. => 구간이 예제처럼 5개 5개로 나뉘어 지는게 아니라, 4개 6개로 나뉘어짐
      - 적절한 mid 값을 가지지 못하여 무한 루프에 빠지게 됨

int a[10] = {2, 7, 11, 11, 16, 19, 22, 22, 22, 32};
int n = 10;

int func(int target, int len){
    int st = -1;
    int en  = len -1;
    while(st < en){
        int mid = (st + en) / 2;
        if(a[mid] < target){
            st = mid;
        }else{
            en = mid - 1;
        }
    }
    return st;
}

이때, func(16, 10)을 호출하여 16에 대한 이분탐색을 해보면, 무한루프에 빠지게 됨

떡볶이 떡 만들기 예제

오늘은 떡볶이 떡을 만드는 날이다. 떡의 길이는 일정하지 않으므로 절단기에 높이(H)를 지정하고 잘라서 맞추려고 한다. 이때 자르고 남는 길이는 손님에게 주려고 한다.예를 들어, 높이가 19, 14, 10, 17cm인 떡이 있고, 절단기 높이를 15cm로 가정하면 자르고 남는 떡의 길이는 4, 0, 0, 2cm이고 총 6cm이다. 손님은 6cm를 가져간다. 이때, 손님이 요청한 길이가 M일 때 적어도 M 만큼의 떡을 얻기 위해 절단기에 설정해야 하는 높이 H의 최댓값을 구하는 프로그램을 작성하시오. (1≤N≤1,000,000, 1≤M≤2,000,000,000, 1≤H≤1,000,000,000 )

파라매트릭 서치 Parametric Search란, 최적화 문제를 결정 문제로 바꿔 해결하는 기법을 말한다.
‘범위 내에서 조건을 만족하는 가장 큰 값을 찾는 것’이 최적화 문제.
‘값을 바꿔가며 ‘조건을 만족하는가?’를 결정하는 것’이 결정 문제.
절단기 높이가 10억까지 가능하니까 1부터 10억까지 완전탐색하면 절대 안된다.
이 문제를 결정 문제로 바꾸기 위해서는 절단기 높이 H를 최소 범위와 최대 범위 사이에서 이진 탐색 처럼 바꿔주며 판단해야 한다.

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int n, m;

vector<int> arr;

int main(){
    cin >> n >> m;
    
    for(int i=0; i<n; i++){
        int x;
        cin >> x;
        arr.push_back(x);
    }

    sort(arr.begin(), arr.end());

    int start = 0;
    int end = 10e9;
    int result = 0;

    while(start <= end){
        long long int total = 0;
        int mid = (start + end) / 2;
        for(int i=0; i<n; i++){
            if(arr[i] > mid){
                total += arr[i] - mid;
            }
        }
        if(total<m){
            end = mid - 1;
        }else{
            result = mid;
            start = mid + 1;
        }
    }
    cout << result << '\n';

}

Algorithm